DS n° 11 1S 3 juin 2009

    SUJET     du     DS n° 11                        Mercredi 3 Juin 2009           1S1

--------------------------------------------------------------------------------------------------------------------------------------------------------       

 Nom :  ............                             50 mn                        Date :  ..........        Classe : ............

 ------------------------------------------------------------------------------------------------------------------------------------------------------

  • Soit la suite ( u ) définie sur IN par :  u0  = 3  et   un + 1   = ( 3 / 4 )  un   + 1 / 2    pour tout  n dans IN .

      Soit    vn   =  un   -  2    pour tout  n dans IN .

     •  •  Montrer que la suite ( v ) est géométrique de raison  3 / 4.                                                             1 point

              ................ 

 

   ............................   

 

 

  • • Donner  vn   en fonction de n .                                                                                                             1 point

        ...........

  

 • •  Exprimer  un  en fonction de  n.                                                                                                           0,5 point

 

     .......................

 

 

 • • Les suites   ( u ) et  ( v ) convergent-elles ?                                                                                            0,5 point

 

        .....................

  

                                                                                                                                                                     0,5 point

 ............................

----------------------------------------------------------------------------------------------------------------------------------------

   •  Soit la suite (w )  définie par :    w0 = 1 / 2     et            wn + 1  =  wn + 1    pour tout   n dans IN. 

      • •  Que peut-on dire de cette suite ?                                                                                                   0,5 point

        ................

 

    • •    Donner son sens de variation.                                                                                                        0,75 point

 

             ....................

 

 

 

    • •  Donner son terme général en fonction de n .                                                                                   0,75 point

 

     ........................

 

 

  • Soit la suite ( k )   telle que :   kn =  (  4 n + 3     ) /  ( 3 n + 2  )   pour tout n dans IN . 

   • •  Donner son sens de variation.

 

 .........................


  ...............                                                                                                                                                1 point

 

 

    • • Donner   lim  kn      .

                                n  →  +∞

 

 

   ..................                                                                                                                                            1 point      

 

 

   •  Soit la suite ( h )  définie par : h0 = 10  et    hn + 1   =   0,6   hn   +  + 2   pour tout  n dans IN.  

   • •  Tracer  les droites  D : y = x  et D' : y = 0,6 x + 2  dans un repère orthonormal.       

 

                                                    

                                                                                                                                                               1,25 point  

  • •    Faire le Web de la suite pour représenter    h1  ,    h2    ,   h3   sur l'axe des abscisses.                       0,75  point

 

 • • Que pouvez -vous conjecturer pour le sens de variation de la suite ( h  ) ? ( Expliquer.)  

                                                                                                                                                                                                                                                           

  ................                                                                                                                                               0,5 point

 

 

 

  • Une balle élastique remonte au  2 / 3  de la hauteur où elle est lâchée.

     Soit   L0  =  2  m  la hauteur où elle est lachée au départ. Soit   Ln   la hauteur de la balle après n

     rebonds. ( n dans IN . )

   • • Trouver   Ln  en fonction de n.                   .                                                                                                 

    

      ....................                                                                                                                                      1 point

 

   • • Trouver le plus petit entier n  tel   Ln   <  0, 1.

   ....                                                                                                                                                          1 point 

  

 

 

 

   • Dessiner la section du tétraèdre ABCD  avec le plan ( IJK ).

       

   

            

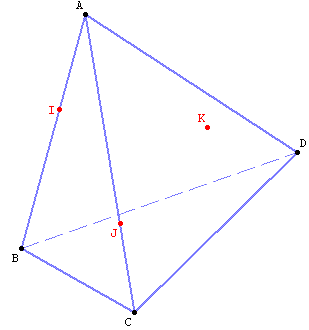
                                                                                                                                                                3 points

 

 

          K est dans la face ( ABD ) . I et J sont respectivement sur les arêtes [ AB] et [ AC].

           Justifier.

 

            .................................

 

   

      •  •  Représenter la droite d'intersection des plans ( IJK ) et ( BCD ) sur la figure .  Justifier.                   4 points

 

    .....

 

 

 

                                                                                                                                                                   RD     1

  ---------------------------------------------------------------------------------------------------------------------------------------------------------------