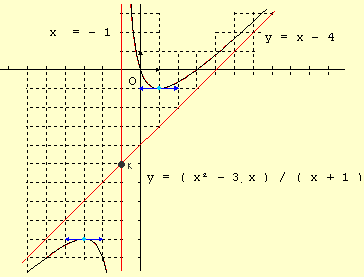SPE TES
Espace membre
TS Sujets
BAC S JUIN 2010
- Bac 2010. S. Ex 1 partie A
- INFOEX1 Partie B BAC S JUIN 10
- EX2 BAC S GRAPHIQUE 22 juin 10
- INFO EX2 1 ROC BAC S JUIN 10
- INFO EX2 2.a. BAC S juin 10
- INFO EX2 2b. BAC S JUIN10
- INFO EX2 2.c. BAC S juin 10
- INFO QUESTION3 EX2 S JUIN 10
- INFO QCM EX 3 BAC S JUIN 2010
- INFO EX4 BAC S JUIN 2010
- INFO EX4 FIG BAC S 22 JUIN 10
- INFO Ex 4 spé Bac S Juin 2010
- INFO EX 4 SPE BAC S JUIN 2010
- TEXTE EXERCICES BAC S 2010
Pages
- INFO LISTE 3 EX ALGO
- TEST 2 COMPLEXES
- SUR ORDI . GEOM. ESPACE 1S
- ACT.VECT. ESPACE 1 S 27MAI 09
- ACT;GEOM. ESP. LUNDI 25 MAI 1S
- INFO DS n° 11 1S 3 juin 09
- Statistiques
- STAGE BTS1 SEPT . 09
- INFO TRAVAIL3 ORDI .GEO. ESP
- INFO ACT GEOM ESP 25 MAI 09 1S
- INFO TRAVAIL 1 ORDI. GEOM ESP
- I ST. BTS
- GEOM. ESPACE 1S MAI 09
- DS n° 11 1S 3 juin 2009
- AIDE STAGE BTS1
- AIDE 2 STAGE BTS 1
- INFO EX 1 Feuille d'ex sur les
- 1.COURS SUITES TS sept 2012
- INFO DS n° 2 TS 27 oct. 2012
- INFO EX2 DV n°5 TS1 27 novemb
- INFO TEST ALGO EX1 27 nov 2012
- INFO TEST ALGO EX5 27 nov 201
- INFO TEST EX Ln Exp TS1 26
- Leçon ...n°7 Calcul intégral
- PYTHON 2.7 TEST BTS1 11/
- Cours : Proba.conditionnelles
- TS INFO EX4 BAC BLANC TS 15/2/
- INFO EX4 BAC BLANC 12 fév 2015
- t
- t
- INFO DEVOIR 22 mars 2016
- INFO EX 4 S 2016
- INFO EX2 DV TS spé maths
- INFO DV n° 5 TS spé 24 janv
- TEST TS spé math du 21 mars 2
- Petit Th. de Fermat TS spé ma
- SUJET BAC S Juin 2019
- Nombre de combinaisons à l'aid
Leçon 1 1S1
- ACTIVITE PREPARATOIRE
- Aide:Activ. prépar.Leçon1 1S
- INFO LISTE 2 EX ( Suite 2)
- INFO 2 TEST1 1S 1 ES OCT 10
- Aide Dv n° 1 1S sept 09
- INFO DV n° 1 Sept. 09 1S
- INFO 2 DV n° 1 Leçon 1 1S1
- INFO 3 DV n° 1 Sept. 09 1S
- DS n°1 1S1 7 / 10 / 09
- INFO 1 DS n° 1 1S1 07/10/09
- INFO 2 DS n° 1 1S1 7/10/09
- INFO3 DS n°1 1S1 07/10/09
- QUESTION LIBRE 1 1S1
- NOTES DS n ° 1 07 / 10 / 09
- INFO Activ .prépar 1S sept 09
- TEST 1 S et 1 ES Oct 2010
- INFO TEST 1 1S et 1ES
- INFO LISTE 2 EX ( Suite)
- INFO LISTE 2 d'EX Leçon 1
- LISTE 2 EX Leçon 1
- INFO LISTE II D'EX Leçon 1
- LISTE II D'EX Leçon 1
- QCM
- QCM
- QCM
- QCM :Fonctions- Enchaînements
- INFO LISTE D'EX
- SERIE 1 LISTE EX
- Leçon 1 ( Suite) 1S
- Fonctions ( Suite de la leçon)
- Fonctions 1S1
- INFO Activ .prépar 1S sept 09
Leçon 2 1S1
- LISTE A EX BARYCENTRE 1S
- INFO LISTE A EX BARY. 1S1
- DS n° 2 1S1 21 / 10 / 09
- INFO1 DS n°2 21/ 10/ 09 1S1
- INFO 2 DS n°2 21/10/09 1S1
- INFO 3 DS n° 2 21/10/09 1S1
- PARTIE FACUL. DS n° 2 21/10/09
- TRANSFORMATIONS ET BARYCENTRES
- INFO Complé. DS n°2 21/10/09
- NOTES DS n° 2 21/10/09 1S1
- QCM BARYCENTRE
- DV n° 2 1S1 24/10/09
- AIDE POUR LE DV n° 2 1S1
- INFO 1 DV n° 2 1S1 24/10/09
- INFO 2 DV n°2 1S1 24/ 10/09
- INFO 3 DV n°2 1S1 24/10/09
Leçon 3 1S1
- DV n°3 1S1 28 / 11/ 09
- AIDE 1 DV n° 3 1S1 nov.09
- INFO1 EX 74 ANGLE ORIEN.TRIGO
- INFO2 EX 74 ANGLE ORIEN. TRIGO
- EXERCICE 74 ANGLES ORIEN.TRIGO
- INFO EX 72 ANGLES ORIEN.TRIGO
- EXERCICE 72 ANGLES ORIEN TRIGO
- INFO EX 71 ANGLES ORIEN.
- EXERCICE 71 ANGLES ORIENTES
- INFO 4 DV n° 3 1S1 28 no. 09
- INFO 5 DV n° 3 1S 28 nov 09
- NOTES DS n ° 3 18 / 11 / 09
- INFO 3 DV n° 3 1S1 28 nov 09
- INFO 2 DV n° 3 1S1 28nov 09
- INFO 1 DV n°3 1S1 28 nov 09
- INFO 4 DS n° 3 1S1 18/11/09
- INFO EX 3 DS 3 1S1 18 nov 09
- INFO EX2 DS n° 3 1S 18 nov 09
- INFO 1 DS n° 3 1S1 18/11/09
- DS n 3 1S1 18 /11 / 09
- INFO5 FEUILLE EX ANGLES ORIEN.
- INFO 4 FEUILLE EX ANGLES ORIEN
- INFO3 FEUILLE EX ANGLES ORI.
- INFO2 Feuille EX ANGLE ORIEN.
- INFO1FEUILLE EX ANGLES ORIEN
- FEUILLE D' EX ANGLES ORIENTES
- AIDE 2 DV n° 3 1S1 09
Leçon4 1S1
- COORDONNEES POLAIRES
- LISTE D' EX. ANGLES ORIENTES
- NOTES DS n ° 4 19 / 12 / 09
- MODULO
- INFO LISTE EX ANGLE ORIEN TRIG
- Liste d'ex: Angle Orien. Trigo
- CHARIOT SUR UNE PENTE
- INFO QCM ANGLES ORIENTES TRIGO
- QCM ANGLE ORIENTE TRIGO. 1S1
- INFO EX ANGLE ORIEN 1S Déc.
- EXERCICE ANGLE ORIEN. Déc.09
- INFO DS n° 4 1S1
- DS n° 4 1S1 19 déc. 09
- FORMULES TRIGO. 1S1 DEC. 09
- INFO 2 LISTE EX TRIGO 1S1 DEC
- INFO 1LISTE:EX TRIG 1S1 Déc 09
- LISTE EX TRIGO 1S1 DEC . 09
- AIDE2 DV n° 4 1S1 janv.10
- AIDE DV n° 4 EX1 1S1 janv.10
- DV n°4 1S1 06 / 01/ 10
- INFO I LIST EX ANGLE ORIEN
- INFO 2 LISTE EX ANGLE ORIENTE
Leçon 5 1S1
- QCM TRIGO ET PROD SCAL
- QCM PRODUIT SCALAIRE
- INFO EX 4 DS 5 1S 27 JANV 10
- NOTES DS n ° 5 27 / 01 / 10
- INFO EX3 DS n° 5 1S 27/01/10
- INFO EX2 DS n° 5 1S 27/01/10
- INFO EX1DS 5 1S1 27/1/10
- INFO Question 1 EX2 DV5 Janv
- INFO Question 2 et 3 EX2 DV5
- INFO EX1 DVn°5 1S 23 JAN 10
- RESULTANTE EN PHY. Janv.10
- AIDE4 DV n° 5 1S1 janv.10
- AIDE3 DV n° 5 1S1 janv.10
- AIDE 2 DV n° 5 1S1 janv.10
- AIDE1 DV n° 5 1S1 janv.10
- DV n° 5 1S1 23/01/010
- INFO2 DV 4 6 janv 10 1S
- INFO1 DV n° 4 6 janv. 10 1S
- OLYMPIADES DE MATHS. SUJETS
- INFO 3 SERIE EX PROD SCAL
- INFO2 SERIE EX PROD SCAL
- INFO 1 SERI E EX PROD SCAL
- SERIE EX PROD SCAL 1S JANV10
Leçon 6 1S1
- AIDE DV n° 6 1S 17 /02/10
- Syst. lin. à deux inconnues
- INFO 3 DV n° 6 1S 17 fév 2010
- INFO 2 DV n° 6 1S 17 fév 2010
- INFO DV n° 6 1S1 17 fév 09
- Notes premier trimestre 1S
- Notes second trim. 1S
- NOTES DS n ° 6 17 / 02 / 10
- QCM SUR LA DERIVATION
- QCM DERIVATION 1S
- INFO EX DERIV. 1S mars 10
- EXERCICES DERIV 1S MARS 10
- EX Dériv. 1S mars 2010
- FEUILLE D' EX 20 fév. 2010
- FEUILLE D' EX 20 fév. 2010
- INFO 3 DS n° 6 1S1 17/02/10
- INFO 2 DS n° 6 1S1 17/02/10
- INFO 1 DS n° 6 1S1 17/02/10
- DS n° 6 1S1 17 février 2010
- INFO 2 FEUILLE EX 1S 12/ 2/10
- INFO FEUILLE EX 1S 12/02/10
- DV 6 1S 17/02/10
Leçon 7 1S1
- QCM DERIVATION 1S Mars 2010
- DV n ° 7 1S1 27 MARS 2010
- RESUME 3 COMPORTEMENT ASYMPTO.
- RESUME II COMPORT.. ASYMPTO.
- RESUME 1 COMPORTEMENT ASYMPTO.
- INFO EX4 SUJET COMMUN 1S
- INFO EX2 SUJET COMMUN 1S
- INFO EX 3 SUJET COMMUN 1S
- INFO QCM SUJET COMMUN 1S
- SUJET COMMUN 1S 2 AVRIL 2010
- INFO2 TEST DER-LIM 1S 27/03/10
- INFO TEST 1S1 27/03/10
- TEST DERIV-LIM 1S1 27/03/10
- INFO4 LISTE EX LIM-DERIV 1S
- INFO 3 LISTE EX LIM-DERIVE 1S
- INFO 2 LISTE EX LIM-DERIV 1S
- INFO 1LISTE EX LIM-DERIV 1S
- LISTE EX 1 S LIMITE-DERIVEE
- AIDE 4 DV n° 7 1S 27 mars 10
- AIDE 3 DV n° 7 1S 27 mars 10
- AIDE 2 DV n° 7 1S1 27/03/10
- AIDE 1 DV n° 7 1S 27 mars 10
Leçon 8 1S1
- INTERRO. LIMITES 1S AVRIL 10
- INTERRO. DERIV-LIMI 10/4/10 1S
- QCM LIMITES
- SUITES NUMERIQUES 14 /04/ 10
- INFO EX N°46 pour le 16/04/10
- EXERCICE N°47 pour le 16/04/10
- EXERCICE N°48 pour le 16/04/10
- EX n°46 n°47 n°48 1S SUITES
- NOTES DS COMMUN 1S 02/04/10
- INFO 1 INTERRO DERIV-LIM 1S
- INFO 3 INTERRO DERIV-LIM 1S
- INFO 2 INTERRO DERI-LIMI1S
- EX Suites 1S1 17 04/10
1S1 Leçon 9
- INFO 1 DV n° 7 1S 27 mars 2010
- INFO 3 DV n° 7 1S 27 mars 2010
- UTILISATION DES SUITES
- INFO EX III PROBA 1S
- EX III PROBA 1S
- INFO EX II PROB. 1S1
- EX II PROB. 1S1
- INFO EX PROBA 1S
- EXERCICE PROBA. 1S
- Année 2009 - 2010 1S
- 3 ième TRIM. 1S
- NOTES DS n ° 9 26/ 05 / 10
- INFO DS n° 9 1S1 26 MAI 2010
- DS n° 9 1S1 26 MAI 2010
- INFO UTILISATION :SUITES
- NOTES DS n° 8 1S
- QCM n° 3 SUITES NUMERI.1S
- QCM n° 2 SUITES NUMERI.1S
- AIDE DV n° 8 1S 28 mai 2M10
- DV n° 8 1S1 28/05/ 2010
- INFO 2 DS n° 8 12Mai 2010 1S1
- INFO 1DS n° 8 12 Mai 2010 1S1
- DS n° 8 12 Mai 2010 1S1
- EXERCICE 1S SUITES MAI 2010
- INFO 4 DV n° 7 1S 27 mars 10
- INFO 2 DV n° 7 1S 27 Mars 2010
- Remarque
1S TS BTS SUITES
- LISTE D'EX. SUITES BTS1
- Cours: SUITES NUMERIQUES 1S
- SUITE I CALCULATRICE TI 84
- INFO EX 4 LISTE 2 SUITES MAI
- EX BAC S 2004 SUITES
- LISTE 2 EX SUITES 1S MAI 09
- INFO EX1 SUITES ADJACENTES
- II SUITES GEOMETRIQUES
- INFO EX4 DS 10 1S MAI 09
- INFO EX BAC S 2004 SUITES
- INFO EX 2 LISTE 2 SUITES MAI
- Web SUR TI 84
- INFO EX 2 SUITES ADJACENTES
- LISTE 1 D'EXERCICES. SUITES
- INFO EX 5 DS 10 1S MAI 09
- EX BAC SUITE TS
- QCM n° 1 SUR LES SUITES
- INFO FEUILLE PROGRAMMEE SUITES
- INFO EX 3 SUITES ADJACENTES
- I I I SUITES ARITHMETIQUE
- DS n° 10 23 MAI 2009 1S
- INFO EX 3 DS 10 1S MAI 09
- INFO EX1 LISTE 2 SUITES MAI
- EX 1, 2 ,3 SUITES ADJACENTES
- INFO LISTE 1 EX SUITES
- COMPLEMENTS TS SUITE NUMERIQUE
- INFO EX1 DS10 1S MAI O9
- INFO EX 3 LISTE2 SUITES MAI
- INFO EX4 SUITES ADJACENTES
- INFO FIN liste 1 SUITES
- SUITES ADJACENTES TS
- SUITE 2 TI 84
- INFO EX 2 DS10 1S MAI 09
- Devoir n° 1 TS1 7 sept 2013
- INFO DV n° 1 TS1 7 sept 2013
- Cours Suites TS sept 2013
- FEUILLE D'EX n°1 SUITES TS1 SE
- INFO FEUILLE D'EX n°1 SUITES T
- FEUILLE D'EX n° 2 SUITE TS1 S
- TEST COURS SUITES TS
- INFO TEST COURS SUITES TS
- INFO FEUILLE D'EX n°2 SUITES T
- AIDE pour le DV n° 2 TS1 04
- Devoir n° 2 TS1 4 octobre 20
- INFO Devoir n° 2 TS1 4 octob
- FEUILLE D'EXERCICE n° 3 SUITE
- TEST SUITES TS OCT 2013
- DS n° 1 11 /10/13 TS1
- INFO 1 DS n° 1 11 /10/13 TS
- INFO 2 DS n°1 TS1 11 oct 2013
- TABLEAU D'HONNEUR DS n° 1 TS1
1S DERIVATION
- LISTE 1 D' EX . DERIVATION
- INFO EX. 3 DERIVATION 1S
- INFO DV n° 5 EX 7 DERIV 1S
- INFO LISTE 5 EX DERIV 1S
- INFO LISTE 4 EX 6 DERIV 1S
- INFO LISTE 4 EX DERI 1S
- LISTE 5 D'EX. DERIVATION 1S
- INFO DV n° 4 1S 29 NOV.
- LISTE 3 D'EX. DERIVATION 1S
- LISTE 4 D'EX. DERIVATION 1S
- INFO. EX 3 DS 3 1S 22 Nov
- INFO. EX 4 DS 3 1S 22 Nov
- INFO. EX 2 DS 3 1S 22 Nov
- INFO. EX 1 DS 3 1S 22 Nov
- QCM 1 DERIVATION 1S
- DV n° 4 1S DERIV. NOV.
- INFO LISTE 2 EX DERIV 1S
- LISTE 2 D'EX. DERIVATION 1S
- EX 3 DERIVATION 1S
- INFO LISTE 1 EX . DERIV . 1S
1S ANGLES, ARCS , ORIENTES OU NON
- INFO LISTE 1 EX ANGLE ORIEN
- LISTE 1 EX ANGLE ORIEN 1S
- ANGLES ORIENTES TRIGO
- DV n° 7 1S
- INFO DV n° 7 1S 9 Mars
- INFO EX 2 DS6 1S1 14 /2/ 09
- INFO EX1 DS n°6 14 /2/ 09
- EX TRIGO 1S Mars
- FORMULAIRE TRIGO
- DS n° 7 1S 1 14 FEV. 09
- INFO DS 7 1S1 14 Mars 08
- EX SIN ' cos '
- INFO EX SIN ' COS '
- I. ANGLE , ARC ORIENTE OU NON
1S PRODUIT SCALAIRE
- PROD . SCALAIRE 1 S Mars 09
- INFO LISTE1 PRO. SCA MARS 09
- RESUME PRODUIT SCALAIRE
- EX 12 PROD SCAL 1S AVRIL 09
- INFO 2 DV n° 7 1S 27 mars 10
- EX 13 PROD SCAL 1S AVRIL 09
- EX 14 PROD SCAL 1S AVRIL 09
- EX 15 PROD SCAL 1S AVRIL 09
- EX 16 PROD SCAL 1S AVRIL 09
- LISTE 2 PROD SCAL 1S AVRIL 09
- ACTIVITE PROD SCALAIRE
- INFO EX 11/ 04 /09 Stagiaire
- EX 11/ 04 /09 Stagiaire
- EX 04/04/09 stagiaire
- INFO EX 04/04/09 Stagiaire
- INFO EX2 DS9 1S 2 MAI 09
- INFO EX 1 DS 9 1 S 2 MAI 09
- INFO EX 3 DS 9 1 S 2 MAI 09
- INFO EX 4 DS 9 1 S 2 MAI 09
- INFO EX 5 DS 9 1S 2 Mai 09
- QCM n ° 1 PRODUIT SCALAIRE
- INFO 2 DV n° 7 1S 27 mars 10
- INFO 2 DV n° 7 1S 27 mars 10
- EX1 PROD SCAL 1S AVRIL 09
- LISTE 1 EX PROD SCAL MARS
- INFO EX 5 6 7 8 PROD SCALAIRE
- TRAVAIL 1S1 SAMEDI 28 MARS 09
- INFO ACTIVITE 28 MARS 09
- INFO 4 DS 1S1 04/04/09
- INFO EX 5 DS 1S1 04/ 04/ 09
- INFO EX1 DS 1S1 04/04/09
- Sujet Commun 1S 04 / 04 /09
- INFO EX 2 DS COMMUN 4/4/09 S
- INFO EX 3 DS COMMUN 4/4/09
- EX 11 PROD SCAL 1S AVRIL 09
- EX 2 PROD SCAL 1S Avril 09
- EX3 PROD SCAL 1S1 AVRIL 09
- EX4 PROD SCAL 1S1 AVRIL 09
- EX 5 PROD SCAL 1S AVRIL 09
- EX 6 PROD SCAL 1S AVRIL 09
- EX 8 PROD SCAL 1S AVRIL 09
- EX 7 PROD SCAL 1S AVRIL 09
- EX 9 PROD SCAL 1S AVRIL 09
- EX 10 PROD SCAL 1S AVRIL 09
1S LIMITES
- COMPORTEMENT ASYMPTOTIQUE 1S
- COMPORT. ASYMPTOTIQUE 1S
- ACTIVITE PRELIMI. LIMITES
- INFO EX 2 DS 5 1S J 09
- INFO EX 1 DS N° 5 1S 1
- DS N° 5 1S 1 24 janvier 09
- INFO DV6 1S JV 09
- INFO LISTE 2 EX LIMITES 1S
- INFO DV6 1S JV 09
- LISTE 2 D'EX LIMITES 1S
- INFO EX6 LISTE 1 1S LIMITES
- INFO EX7 LISTE 1 1S LIMITES
- INFO EX 5 LISTE 1 1S LIMITE
- INFO LISTE 1 EX 1 . 2. 3 . 4
- INFO EX2 DS4 1S 20 Déc.08
- INFO EX3 DS4 1S 20 Déc 08
- INFO EX 1 DS4 1S 20 Déc 08
- EX LIMITES 1S Janv. 09
- COMPORT. ASYMPTOTIQUE 3 1S
1ES Devoir et Exercices
- DS n° 6 1ES - L 11 février 2
- DEVOIR MAISON 1 ES- L 28/01/1
- DEVOIR MAISON 28/01/1012
- INFO DS 1 ES 17 /12/11
- DS 1ES DS 2 17 / 12/
- INFO DV MAISON 1ES-L 17/12
- DV MAISON 1ES-L 17/12/11
- DV maison 1ES Samedi 2 déc. 20
- INFO DV maison 1ES-L Samedi 2
- INFO DS n° 6 1ES-L 11février
- INFO DS n °3 1ES-L
- DS n° 3 1 ES-L 07/11/11
- INFO DV n° 2 Maison du 12 nov.
- EX n° 22 Livre 1ES Hyperbole
- INFO Ex n° 27 page 106
- INFO DS 1ES 29 MAI 2010
- TD de programmation linéaire
- DS n° 1 1ES 10/10/09
- INFO DS n° 1 1ES 10 / 10/09
- DS n° 2 23 / 10 / 09 1ES
- INFO DS n° 2 23/10/09 1 ES
- DS n° 3 1ES 17/11/09
- INFO DS n°3 1ES 17/11/09
- DS 6 avril 2010 1 ES
- INFO DS 6 AVRIL 2010 1 ES
- DS 1ES 29 MAI 2010
- INFO TEST 3 1ES 17 / 11/10
- INFO TEST 1 1ES 29/09/10
- TEST 1 1ES 29/09/10
- TEST 3 1ES 17 / 11/ 10
- INFO TRAVAIL 1ES SEPT 2011
- TRAVAIL 1 1ES SEPT 2011
- COEFFICIENT MULTIPLICATEUR
- TEST 1ES SUITES MARS 2011
- INFO DS 1ES 23/11/10
- DS 1ES 23 / 11/10
1S 1ES TS BTS PROBA.
- EXERCICE 1ES SUR : LOI BINOMIA
- LISTE 1 EX PROBA. BTS1 nov
- INFO LISTE 2 EX . PROB BTS1
- LISTE 2 D'EX. PROB BTS1
- INFO TEST PROBA Fév. 2011
- PROJET 2 BTS1 EX 1
- INFO TRAVAIL BTS MARS 2011
- PROJET 2 BTS1
- EX PROB TS
- INFO 4 TEST PROBA 11 mars 2011
- INFO 3 TEST PROBA 11 mars 2011
- INFO 2 TEST PROBA 11 mars 2011
- INFO 1 TEST PROBA 11 mars 2011
- TEST PROBA 11mars 2011
- TEST PROBA Fév. 2011
- INFO LISTE 1 D' EX PROB BTS1
- INFO TEST 9/2/11 BTS PROB
- TEST PROB Février 2011
- INFO TRAV SUR ORDI JV 09
- INFO TEST ORDI JV 09
- TEST SUR ORDI BTS JV 09
- TRAVAIL SUR ORDI BTS JV 09
- INFO INITIATION VAR BTS1
- INITIATION AUX V.A.R BTS1
- LISTE 3 D'EX BTS1 PROBA.
- INFO LISTE 3 EX PROB. BTS1
BTS1 LOGIQUE
- LOGIQUE ELEMENTAIRE
- LOGIQUE ELEMENTAIRE 1
- LOGIQUE ELEMENTAIRE 2
- Devoir 1 BTS Logique
- INFO DV 1 BTS1 OCT.09
- TEST 2 LOGIQUE BTS1 A 17/10/11
- INFO TEST 2 LOG BTS1 A 17/10/
- INFO TEST 2 LOG BTS1 B 21
- TEST 2 LOG BTS1B 21/10/1
- D. AVAKOV : 09/10
- QCM DE LOGIQUE
- EXERCICES DE LOGIQUE
- EXERCICES DE LOGIQUE DE BASE
- INFO EX DE LOGIQUE DE BASE
- QCM DE LOGIQUE 3
- TEST n°6 LOGIQUE
- INFO TEST n° 6 LOGIQUE
- TEST n ° 7 LOGIQUE BTS 1
- INFO TEST n ° 7 LOGIQUE
- CORRECTION DES EX.
- CONTRÔLE TEST 1
- CORRECTION TEST 1
- Contrôle TEST 2 Logique
- INFO . Contrôle TEST 2
- LISTE D' EXERCICES 2 LOGIQUE
- INFO LISTE 2 EX LOGIQUE BTS
- TEST 3 LOGIQUE BTS TS
- TEST n° 5 LOGIQUE
- INFO TEST n° 5 LOGIQUE
- INFO TEST n° 4 LOGIQUE
- TEST n°4 LOGIQUE
- Bases du Second degré
- INFO ACT. Types Raisonnements
- ACTIV: Types de raisonnements.
- INFO TEST 3
- TEST Logique BTS
- INFO TEST Logique
- TEST DE LOGIQUE 15/11/2005 BTS
- INFO TEST DE LOGIQUE 15/11/200
- Exercices de logique
- TEST LOGIQUE BTS1 8/10/14
- INFO TEST LOGIQUE BTS1 8/10/
- TEST 15 octobre 2014
- INFO TEST LOGIQUE 15 /10/14
- TEST 2 LOGIQUE BTS1 A 5/11/14
- INFO TEST LOGIQUE 5 / 11 / 14
- Compléments
- Bijection: surjection: injecti
- E22
- CONVOCATIONS E 22
BTS1 ALGEBRE DE BOOLE
- ALGEBRE DE BOOLE RAPPELS
- DS BTS 1 A SLAM 07/02/
- ALGEBRE DE BOOLE 1
- INTRO. TERTIAIRE ALG. DE BOOLE
- LISTE 1 D' EX . ALGEBRE DE B
- DS n° 1 BTS1A 23/10/09
- INFO DS 13/2/09 BTS1A
- TRAVAIL 3 ORDI BTS FV 09
- INFO TEST ALG.BOOLE 12/11/2010
- INFO LISTE 1 EX ALG BOOLE
- INFO 1 DS n°1 BTS1A 23/10/09
- Proposition ex par BTS1A
- TRAVAIL 4 ORDI BTS FV 09
- TEST ALG. DE BOOLE 12/11/10
- TEST ORDI BTS BOOLE
- INFO 2 DS n°1 BTS1A 23/10/09
- INFO DV n° 1 12 oct. 09 BTS
- INFO TRAVAIL 2 ORD BTS FV 09
- TRAVAIL SUR ORDI BTS FV9
- QCM ALGEBRE DE BOOLE
- INFO TRAVAIL ORDI BTS FV9
- EX ALGEBRE DE BOOLE
- TRAVAIL 2 ORDI BTS FV 09
- TEST ALG. DE BOOLE 2010
- Ex extrait d'un sujet de BTS
- INFO DS n° 1 BTS1B 20/10/09
- DS n° 1 BTS1B 20 / 10 / 09
- INFO TRAVAIL 4 ORD BTS FV 09
- INFO TRAVAIL 3 ORD BTS FV 09
- EXERCICE BTS1 B 30 novembre
- INFO EX 2 TEST BTS1 B 30 nove
- INFO EX 1 TEST BTS1 B 30 novem
- EX 3 BTS1B Décembre 2012
- INFO EX3 TEST BTS1 décembre 20
- TEST n° 2 13novembre 2013
- INFO TEST n°2 13 novembre 2013
- INFO TEST n° 2 du 18 novembre
- TEST n° 2 du 18 novembre 2013
- TEST n° 3 mercredi 20 nov. 201
- INFO TEST n° 3 mercredi 20 no
- INFO TEST n°3 26 novembr
- TEST n°3 26 novembre 2013
- INFO TEST ALG DE BOOLE 11 déc.
- TEST ALG BOOLE 11 déc. 201
- INFO TEST BTS1 A 26 NOV 2014
- INFO TEST BTS1 du 3 décembre
- BULLETIN sem1 dec 2014 BTS1A
- BULLETIN sem1 dec 2014 BTS1B
- INFO EXERCICE 3
- EXERCICE 3
- TEST 1 12 octobre 2016
- DS 1 12 octobre 2016
BTS1 MATRICES et SYSTEMES LINEAIRES
- CALCUL AVEC DES MATRICES
- ACTIV 1 ORDI MATRICES BTS
- TEST MATR.-SYST. nov 09
- INFO EX1 SYSTEME LINEAIRE
- INFO EX 2 SYSTEME LINEAIRE
- INFO EX 3 SYSTEME LINEAIRE
- INFO EX4 SYSTEME LINEAIRE
- EX SUR LES GRAPHES
- INFO EX GRAPHE
- ACTIVITE GRAPHES ORIENTES
- INFO ACTIVITE GRAPHE
- EX GRAPHE 1
- INFO EX 1 GRAPHE
- TEST GRAPHE BTS1
- INFO TEST
- EX3 SYSTEME LINEAIRE
- INFO TEST 20/11/09
- TEST 2 MATR.-SYST. nov 09
- INFO TEST2 MATR. SYST. NOV 09
- TEST MATR.-SYST.GRAPHE déc. 09
- INFOTEST DEC 09 MATRICE-GRAPHE
- INFO TEST BTS1A 1/12/09
- EX SUJET : SYST. MATR. BTS
- EX DE SUJET BTS MATRICE- SUITE
- INFO EX SUJET BTS MATR. SUITE
- TI 84 et MATRICES
- INFO EX3 EPREUVE BTS MATRICE
- TEST BTS1 MATRICES 2010
- ACTIV. SYSTEME LINEAIRE BTS
- INFO ACTIV 1 ORDI MATRICES
- EX 0 EPREUVE DE BTS MATRICES
- INFO EX 0 EPREUVE BTS MATRICE
- SYSTEME EQUATIONS LINEAIRES
- EX 2 EPREUVE DE BTS MATRICES
- INFO EX2 EPREUVE BTS MATRICE
- EX 3 EPREUVE DE BTS MATRICES
- ACTIV.2 ORDI MATRICES BTS
- ACTIV.3 ORDI MATRICES BTS
- ACTIV 4 ORDI MATRICES BTS
- EXERCICE : SYST. LIN Nov 09
- LISTE A D' EX. SYST. 10/11/09
- INFO LISTE A EX SYST. 10/11/9
- EX1 SYSTEME LINEAIRE
- EX4 SYSTEME LINEAIRE
- EX2 SYSTEME LINEAIRE
- INFO EX 5 SYSTEME LINEAIRE
- TEST BTS1B 29/03/13
- INFO TEST BTS1A 11 déc 2013
- TEST MATRICE BTS1 A
- SEMESTRE 1_ 2013 BTS1A
- TEST MATRICES 18 /12/13
- INFO TEST 18/12/13
- INFO EXERCICES 3 bis
- EXERCICE SYST 26 Nov 2014
- EXERCICE sur les matrices et s
- TEST BTS 1 du 3 février 2016S
- INFO TEST 3 Février 2016
- INFO TEST n°2 BTS1 B 17 fév
- INFO TEST n°2 BTS 1 A 17 févri
- TEST n° 2 BTS1 A 17 février 20
- TEST n°2 BTS 1 B 17 février 20
BTS1 SUJETS
- SUJET 2009 BTS
- INFO EX 1 SUJET 2009 BTS
- ALERTE BTS SESSION 2009
- EX3 BTS SESSION 2009
- INFO EX2 A BTS SESSION 2009
- INFO EX2 B BTS SESSION 2009
- INFO EX 2 C BTS SESSION 2009
- BTS SIO 2017 sujet
- INFO SUJET BTS SIO 2017
- INFO Maths.approfondies ex 1 B
- Sujet Math.approfondies BTS SI
- INFO Maths.approfondies ex 2 B
BTS1 GRAPHE ORIENTE 2
- INFO EX 00 SUR LES GRAPHES
- EX 00 SUR LES GRAPHES
- LISTE EX SUR LES GRAPHES
- INFO EXGRAPHE EPREUVE BTS FR0
- DS BTS1 B 10 AVRIL 09
- EX III SUR LES GRAPHES
- TEST GRAPH BTS Déc. 2010
- INFO EX III SUR LES GRAPHES
- INFO TEST GRAPH Déc. 2010
- DS BTS1 10 Avril 2009
- INFO LISTE EX SUR LES GRAPHES
- INFO DS 10 AVRIL 09 BTS1A
- EX GRAPHES EPREUVE BTS FR00
- INFO DS BTS1B 10 AVRIL 09
- TEST GRAPHES janvier 2014 BTS
- INFO TEST GRAPHE janvier 2014
- TEST2 GRAPHE 28 janvier 2014
- INFO TEST 2 28 janvier 2014
- TEST 5 GRAPHE BTS 2014
- INFODEBUT TEST 5 GRAPHE BTS
- TEST 6 GRAPHE BTS1 janvier 14
- INFO TEST 6 GRAPHE BTS1 janvie
- TEST BTS1B 21 janvier 2015
- INFO TEST BTS1 B 21 janvier 20
- TEST BTS1 A mercredi 21 janvie
- TEST BTS1 A 4 février 2015
- INFO TEST BTS1 A 4 février 201
- INFO EX 2 TEST BTS1A janvier
- EX1 TEST BTS1 B 11 février 20
- INFO EX1 TEST BTS1 B 11 févri
- EX2 TEST BTS1 B 11 février 201
- INFO EX2 TEST BTS1 B 11 févri
- Sujet Nouvelle calédonie
BTS1 VARIABLES ALEATOIRES
- PROBA: VARIABLES ALEATOIRES 1
- PROBA: VARIABLES ALEATOIRES 2
- V.A.R. DE LOI NORMALE
- INFORMATION EXERCICES
- EX 1 DU SUJET 2003
- INFO TEST 5 SUR V.A.R
- CORRECTION EX: LOIS NORMALES
- INFO LISTE EX . VAR.
- INFO TEST 4
- Contrôle TEST STAT. PROBA.
- INFO TEST 3
- INFORMATION EX 1 SUJET 2003
- EXERCICES ( LOI S NORMALES. )
- EX 3 BTS SUJET 2000
- EXERCICES SUR LES V.A.R
- TEST V.A.R 4
- TEST 5 V.A.R
- INFO TEST 2 PROBABILITE
- LISTE EX . VAR
- QCM 1
- LISTE 2 EX . LOIS NORM.
- Contrôle TEST 3
BTS1 DENOMBREMENTS
- EX. 1 SUR LES DENOMBR.
- EX 2 SUR LES DENOMBR.
- EX 4 SUR LES DENOMBR.
- TEST BTS1A 26/01/10
- REMARQUE DS BTS1 22/1/10
- INFO EX1 TEST BTS 1 26/01/10
- INFO EX2:TEST BTS 1 26 janv10
- INFO EX4 TEST BTS1 26 JANV
- INFO EX3 TEST BTS1 26 JANV
- DV BTS1 5/ 02 / 10
- INFO DV BTS1 5 février 210
- TEST BTS 2010
- INFO TEST BTS1 15 / 02/10
- TEST BTS1 DENOM-PROB f 2008
- INFO TEST BTS1 16/02/10
- TEST BTS1 DENOM-PROB 16/2/2010
- INFO TEST DENO-PRB BTS 16/2/10
- INFO EX4 BAC S JUIN 2010
- TEST BTS1 26/01/11
- INFO TEST BTS 1 26/01/11
- DS-TEST BTS1 22/01/2010
- DENOMBREMENTS 1
- PROBLEMES DE DENOMBR.
- INFO PROBLEMES DENOMBR. BTS
- DS 2 BTS1B 19 nov 0 8
- INFO DS 2 BTS1B 19 NOV. 08
- LISTE 2 D'EX. DENOMBR. BTS
- INFO LISTE2 EX DENOMB BTS
- DS 2 BTS1A 28 nov 08
- INFO EX1 DS 2 BTS1A 28 NOV.
- INFO EX 3 ; 4 ; 5 DS2 BTS1A
- INFO EX 2 DS2 BTS1A
- INTERRO. COURS. BTS1 DENOMBRE
- INFO INTERR. COURS DENOMB.
- INFO DS BTS1 22/01/20010
- Nombre de combinaisons à l'aid
- COMPLÉMENTS SUR LES DENOMBREM
- COMBINAISONS AVEC RÉPÉTITIONS
- INFO COMBINAISONS AVEC RÉPÉTI
SPE MATHS TS 2016 -2017
- INFORMATION SUR LE BINÔME DE N
- TEST n° 2 MATRICES Spé maths
- INFO TEST n° 2 MATRICES Spé
- Notes TEST N ° 2
- DV n° 2 TS spé maths
- INFO DV n ° 2 TS spé maths
- FEUILLE D'EXERCICES sur les g
- SUITE DE LA FEUILLE D'EX sur
- Notes TEST N ° 3
- INFO TEST n° 3 Spé maths TS
- TEST n° 3 Spé maths TS
- Remarque devoir maison n°4
- DV n °4 TS Spé maths déc.2015
- INFO Devoir maison n°4 TS s
- Remarque
- EXERCICE 1 : restes et con
- EXERCICE 2 sur les congruenc
- EXERCICE 3 sur les congruences
- EXERCICE 4 sur les diviseurs.
- DV du 26 janvier reporté au 2
- EX spé 09/ 02/16
- INFO EXERCICE spé
- Bac Blanc 16 février 2016
- DEVOIR DU 22 MARS 2016
- INFO DEVOIR 22 mars 2016
- TEST 29 mars 2016
- INFO TEST du 29 mars 2016
- Notes bac blanc. 14 mai 2016
- INFO EX1 DV spé maths sept
- EX2 DV spé maths sept 2016
- EX1 DV spé maths sept 2016
- INFO EX2 DV TS spé maths
- TEST n° 1 mardi 4 octobre 2016
- Entraînement 4 oct 2016
- TEST n° 2 mardi 18 octobre 2
- INFO Test n ° 2 Mardi 18 octo
- INFO DV n° 2 mardi 18 octob
- Devoir maison n°2 Mardi 1
- TEST n° 3 mardi 8 novembre 2
- INFO TEST 3 mardi 8 nov 201
- TEST 4 22 nov 2016
- INFO TEST 22 novembre 2016
- INFO Devoir 3 22 nov 2016
- DV 4 Spé maths 8 / 12/16
- INFO DV n ° 4 Spé Maths TS
- TEST 5 10 janvier 2017
- INFO TEST 5 10 janvier 2017
- INFO DV n° 5 TS spé 24 janv
- DV 5 du 24 janv. 17 TS spé
- INFO TEST EX1 spé TS 31/1/17
- TEST EX1 spé TS 31 janvier 20
- INFO TEST EX 2 TS spé 31 jan
- TEST EX2 spé TS 31 janv.2017
- DV n° 6 TS spé 28/02/17
- INFO DV n° 6 TS spé 28/02/
- Sujet Bac Blanc 24 février 21
- INFO BAC BLANC 24 fev.2017 spé
- TABLEAU D'HONNEUR
- DV n° 7 TS spé 14/03/17
- INFO DV n° 7 TS spé 14 mars
- Activité carte vitale
- INFO Activité carte vitale
- Activité code barres EAN 13
- INFO activité code barres
- Activité : Chiffrement de VIGE
- INFO activité chiffrement de V
- Nombre de Mersenne.. Nombre pa
- INFO Nombres de Mersenne.Nombr
- INFO TEST TS spé math du 21 ma
- TEST TS spé math du 21 mars 2
- EX sur les ROCS TS spé maths
- INFO EX sur les ROC TS spé ma
- INFO DV n° 8 TS spé du 18 avr
- DV n°8 TS spé math. 18 / 04/1
- INFO ACTIVITE : CARMICHAËL
- ACTIVITE : CARMICHAËL TS
- Petit Th. de Fermat TS spé ma
- INFO Activité: Petit th.de Fer
- INFO :Activité de dem.du petit
- Activité de dem.du petit th de
- INFO EX SPE BAC BLANC du 4 m
- EX Spé Math.TS Bac Blanc 4 ma
- Notes ex 4 bac blanc 4 mai 201
- EX de bac spé S 2017 N.
- FEUILLE D'EX TS spé maths mai
- INFO TEST TS spé maths du 16
- TEST TS spé maths du 16 mai 20
BTS1 NUMERATION
- Cours : numération
- FEUILLE D'EXERCICE sur la numé
- Feuille d'exercices sur la num
- COMPLEMENT A 2
- ENTIER RELATIF EN BASE 2
- TEST 1 NUMERATION BTS1 B
- INFO TEST 1 B_NUMERATION
- TEST BTS1 NUMERATION
- INFO TEST BTS1 NUMERATION
- TEST n° 1 BTS septembre 2011
- EXERCICES DE NUMERATION
- INFO 2 FEUILLE EX NUMERATION
- INFO FEUILLE EX NUMERATION
- FEUILLE EX NUMERATION
- BASE : SYSTEME DE NUMERATION
- ENTIERS NEGATIFS EN BASE 2
- SOMME ET PRODUIT EN B 2
- INFO NUMERATION TRAVAUX BTS1
- NUMERATIO: TRAVAUX A EFFECTUER
- Résumé de cours de numération
- CONVERSION BASE 10 VERS BASE B
- essai
- EX DE NUMERATION BTS1
- INFO EX BTS1
BTS1 ALGORITHMIQUE
- PYTHON.2 FEUILLE D'EX 9
- PYTHON. 2 FEUILLE 4 D'EXER
- RESUME: Python 2.7 utile pour
- FEUILLE D'EX n° 9 bis Dichoto
- PYTHON. 2 INFO Feuille 4
- PYTHON.2 INFO FEUILLE n° 9 D'E
- PYTHO 2.7 RENTREE BTS ALGORIT
- DEBUT en Python.2
- PYTHON 2. FEUILLE n° 9 TER
- PYTHON.2 Feuille 10 :Sujet EXA
- TEST ALGO BTS1B 24 nov. 2014
- Python 2 : Deux modules
- PYTHON 2 INFO FEUILLE 7 EX
- PYTHON 2 FEUILLE n° 10 BIS
- PYTHON. 2 Feuille 1 EX
- PYTHON 2 :Feuille n°5 sur les
- PYTHON .2 FEUILLE n° 3 d'exer
- PYTHON 2.7 TEST BTS1B 4/12/
- BTS1B TEST ALGO 17 nov 2014
- Pyrthon 2 Feuille n° 6 d'exer
- PYTHON .2 FEUILLE n° 2 D'E
- BTS1A TEST ALGO déc.. 2014
- PYTHON.2 FEUILLE D'EX n° 8
- PYTHON. 2 Feuille n°9 QUARTO
- PYTHON. 2 INFO Feuille n° 8 bi
- PYTHON .2 INFO. FEUILLE n°3
- PYTHON 2 FEUILLE n° 7 EX
- PYTHON. 2 INFO Feuille 1 EX
- INFO TEST ALGO BTS1 A déc. 201
- INFO PYTHON 2.7 TEST BTS1B
- PYTHON 2. FEUILLE n° 7 BIS
- PYTHON .2 FEUILLE n° 3 BIS
- PYTHON.2 INFO FEUILLE 10 Sujet
- PYTHON.2 INFO FEUILLE n° 8 D'E
- INFO TEST ALGO 24 nov 2014
- PYTHON 2.7 QUESTIONS
- INFO BTS1 B TEST ALGO 17 nov 2
- PYTHON.2 INFO FEUILLE 2
- PYTHON 2.7 TEST BTS1 11/
- INFO PYTHON 2.7 TEST BTS1 11/1
- PYTHON 2.7 TEST BTS1A 10
- INFO PYTHON 2.7 TEST BTS1A 10
- TEST BTS1 B 1 mars 2017
- TEST BTS1 26 janvier 2016
- PYTHON. 2 PREMIERS EXEMPLES
- PYTHON 2 FEUILLE n° 11 D'EXERC
- PYTHON 2 FEUILLE n° 11 bis D'E
- PYTHON.2 INFO Feuille n°11 D'
- PYTHON 2.7 TEST BTS1A 17/12/
- INFO PYTHON 2.7 TEST BTS1 A 1
- TEST ALGO BTS 28/1/14
- INFO TEST ALGO BTS 28/1/14
- PYTHON 2 INFO FEUILLE n° 12
- PYTHON 2 :Feuille n°12 D'EXERC
- TEST ALGO 5 février 2014
- INFO TEST D'ALGO 5 février 201
- PYTHON 2 FEUILLE n° 13 D'EXERC
- PYTHON.2 INFO FEUILLE n° 13 D
- PYTHON.2 FEUILLE n ° 14 D'EX
- PYTHON.2 INFO FEUILLE n °14 D'
- Python 2 FEUILLE n°15 D'EXERCI
- PYTHON 2 INFO FEUILLE n° 15 D'
- PYTHON.2 FEUILLE n° 16
- PYTHON.2 INFO FEUILLE n°16 D'E
- PYTHON.2 INFO FEUILLE n°17 D'E
- PYTHON.2. FEUILLE n°17
- PYTHON.2 FEUILLE n° 18 D'EXERC
- PYTHON.2 INFO FEUILLE n°18 D'E
- FEUILLE D'EXERCICE n° 19 BTS1
- QCM
- PYTHON.2 INFO FEUILLE n° 19
- TEST ALGO 10 février 2016
- INFO TEST ALGO du 10 février 2
- PYTHON.2 FEUILLE n° 20 D'EXERC
- PYTHON.2 INFO FEUILLE n ° 20
- Entraînement d'algo mardi 8
- INFO Entraînement d'algo. mard
- Entraînement d'algo 9 / 4/14
- INFO Entraînement d'algo. merc
- PYTHON.2. INFO FEUILLE n° 21 B
- PYTHON.2. FEUILLE n° 21 D'EXE
- PYTHON.2. FEUILLE D'EX n°22 BT
- PYTHON.2. INFO FEUILLE n° 22 D
- PYTHON.2 FEUILLE n° 23 D'EX
- PYTHON.2.INFO FEUILLE n° 23 D'
- PYTHON.2. FEUILLE n° 24 D'EX
- PYTHON .2 .INFO FEUILLE n° 24
- PYTHON 2 FEUILLE n° 24 bis su
- PYTHON 2.7 FEUILLE n° 24 Ter
- PYTHON 2 FEUILLE n° 24 quatr
- PYTHON 2 FEUILLE n° 24 quinto
- PYTHON 2 FEUILLE n° 24 six s
- PYTHON 2 FEUILLE n° 24 sept
- PYTHON 2 FEUILLE n° 24 hu
- PYTHON 2 FEUILLE n° 24 neu
- PYTHON 2 FEUILLE n° 24 di
- PYTHON 2 FEUILLE n° 24 11
- PYTHON 2 FEUILLE n° 24 dou
- PYTHON 2 FEUILLE n° 24 tr
- PYTHON 2 FEUILLE n° 24 qu
- PYTHON.2. FEUILLE n° 25 D'EXER
- PYTHON. 2 INFO FEUILLE n° 25
- PYTHON.2.. FEUILLE n° 26 D'EXE
- PYTHON.2.INFO FEUILLE n ° 26 D
- PYTHON.2. FEUILLE n° 27 D'EXER
- PYTHON INFO FEUILLE n° 27 D'EX
- PYTHON.2 FEUILLE n° 28 D'EXE
- PYTHON.2.INFO FEUILLE n° 28
- PYTHON.2 INFO FEUILLE n° 29 D
- PYTHON.2 FEUILLE n° 30 D'EX B
- PYTHON 2. FEUILLE n°31 Matrice
- PYTHON 2. FEUILLE n°32
- PYTHON. 2 FEUILLE n°33
- PYTHON. 2 FEUILLE n°34 d'EX A
- Sous suites convergentes de (s
- PYTHON 2 FEUILLE n°36
- PYTHON 2 FEUILLE n° 37
- IIIIIIIIIIIIIIIIIIIIIIIIIIIIII
- PYTHON. 2 Généralités
- PYTHON. 2 EXEMPLES BASIQUES
- PYTHON.2 COURS D'ALGORITHM
- PYTHON PROCESSUS DE PROGRAMM
- PYTHON. 2 LIEN VERS UN TUTORI
- PYTHON. 2 TEST
- PYTHON .2 TUTORIEL EN FRANCAIS
- PYTHON . 2 RESUME SUR LISTES
- Python . 2 : LISTE
- PYTHON 2 LISTES PAR L'EXEMPLE
- Cours PYTHON 2ou3
- PYTHON.2 TEST 2 EXAMEN BTS 1
- PYTHON.2 INFO TEST 2 EXAMEN BT
- PYTHON. 2 : PYTHON-ALGOBOX COM
- PYTHON2 EX proposé par Tony
- Lien vers les Modules disponib
- IIIIIIIIIIIIIIIIIIIIIIIIIIIIII
- CCF E22 n°8 BTS 1 SIO mai 2
- CCF E22 n°2 BTS 1 SIO mai 2
- CCF E22 n° 1 BTS 1 SIO Mai
- Première page d'un sujet de l'
- ALGO DIRECT
- ALGO DIRECT2
- ALGO TERTIAIRE ALGOBOX
- TEST ALGO n° 1 BTS 1
- TEST 2 AGLO BTS 1
- INFO TEST ALGO n° 2 BTS1
- CONSEIL:REDACTION D'UN ALGORIT
- TEST SIO MARS
- CCF E22 n°4 BTS 1 SIO mai 2
- INFO DECOMPOSITION EN FACTEURS
- ALGO DIRECT3
- INFO TEST 1 ALGO BTS1
- INFO LISTE 4 EX ALGO
- EVALUATION D'UN ALGORITHME D'U
- EX ALGO
- INFO LISTE 3
- INFO LISTE 2 EX ALGO
- LISTE 1 D'EX ALGORITHME
- EX4 ALGORITHME
- EX 5 D'ALGORITHME
- EX 3 D'ALGORITHME
- EX 2 D'ALGORITHME
- EX 1 D'ALGORITHME
- INFO LISTE1 EX 3 ; 4 ; 5 ALGO
- CHARGEMENT D'ALGOBOX
- Ecran ALGOBOX
- INFO EX 5 D'ALGO: DECIMAL vers
- LISTE 4 EX ALGO
- INFO EX 4 ALGORITHME
- INFO EX 3 D'ALGORITHME
- LISTE 3 D'EX ALGORITHME
- INFO EX 2 D'ALGORITHME
- INFO LISTE 2 EX ALGORITHME
- LISTE 2 D'EX ALGORITHME
- INFO EX 1 ALGORITHME
- INFO LISTE1 EX 1 ET 2 ALGO
- EQUATION 2ième DEGRE ALGOBOX
- COURS3 D'ALGORITHMIQUE BTS SIO
- COURS 1 BASIQUE D'ALGORITHMIQU
- COURS 2 BASIQUE D'ALGORITHMIQU
- Feuille 1d'ex.algo."papier
- Feuille 2 d'ex. algo. "papier"
- ALGO permutation circulaire 8
- TEST1 ALGO BTS
- INFO TEST ALGO EX1 27 nov 2012
- INFOTEST ALGO EX2 27 nov 2012
- INFO TEST ALGO EX3 27 nov 2012
- INFO TEST ALGO EX4 27 nov 2012
- INFO TEST ALGO EX5 27 nov 201
- INFO TEST ALGO EX 6 27 nov 20
- INFOTEST ALGO EX7 27 nov 2012
- INFO TEST EX8 BTS1A 27 novembr
- EXERCICE BTS 2011
- INFO EX1 TEST BTS1B 7 déc.2012
- INFO EX2 TEST BTS1B 7 déc 201
- INFO EX3 TEST BTS1B ALGO 7 d
- INFO EX4 TEST BTS1B 7/12/12
- INFO EX5 TEST BTS1B 1LGO 7/12/
- Division euclidienne par soust
- AIDE POUR RECUPERER UNE PARTIE
- TEST ALGO février 2015
- TEST ALGO2 février 2015 et jan
- LE CARRE DE POLYBE
- BTS1 Feuille n° 53
- TEST BTS1 1789
- INFO TEST BTS1 1789
- Proposé par wiliam
- Proposé par zndy
- EX proposé par Guillaume BTS1
- EX sur une idée d'un étudiant:
- Exercice2413
- 424
- METHODE du PIVOT de GAUSS
- Codage de HILL
- TEST ALGO
- Encoding
- SUJET 43 mai 2017
- SUJET 44 mai 2017
- SUJET 45 mai 2017
- SUJET 46 mai 2017
- SUJET 47 mai 2017
- SUJET 48 mai 2017
- SUJET 49 mai 2017
- SUJET 50 mai 2017
- SUJET 51 mai 2017
- SUJET 52 mai 2017
- SUJET 53 mai 2017
- SUJET 54 mai 2017
- SUJET 55 mai 2017
- SUJET 56 mai 2017
- SUJET 57 mai 2017
- SUJET 58 mai 2017
- SUJET 59 mai 2017
- SUJET 60 mai 2017
- SUJET 61 mai 2017
- SUJET 62 mai 2017
- SUJET 63 mai 2017
- SUJET 64 mai 2017
- SUJET 65 mai 2017
- SUJET 66 mai 2017
- SUJET 67 mai 2017
- SUJET 68 mai 2017
- SUJET 69 mai 2017
- SUJET 70 mai 2017
TS NOMBRES COMPLEXES
- INFO DS n° 3 TS2 14 nov 2011
- TEST TS NOMBRES COMPLEXES
- INFO TEST 1 TS2 NB COMLEXES
- TEST RAPIDE TS NB COMPLEXES
- DS n° 3 TS2 14/11/11
- LISTE EX NOMBRES COMPLEXES
- EX FAIT LE 19 OCT 2010 TS2
- INFO DS n°2 Nb Compl 22/10/10
- INFO DS n° 3 TS2 12/11/10
- DV n° 3 TS2 15/11/10
- Réponse à une question posée
- AIDE DV n ° 3 TS2 15 /11/10
- DV n° 2 TS2 1 8 / 10 / 10
- SITUATION AVEC NB COMPLEXES
- INFO DV n° 3 TS2 15/11/10
- INFO DV 2 MAISON TS2 OCT 10
- TEST NB COMPLEXES
- Réponse à une question posée
- DS n°2 Nb Complexes 22/10/10
- INFO TEST NB COMPLEXE
- DS n° 3 TS2 12/11/10
- INTRO NOMBRES COMPLEXES
- Leçon n° 1. Nombres complexes
- EXTRAIT D'EXERCICE DE BAC. Nb
- INFO EXTRAIT D'EX BAC
- PREMIER TRAVAIL A REALISER
- SECOND TRAVAIL à réaliser
- INFO SECOND TRAVAIL
- TROISIEME TRAVAIL A REALISER
- INFO TROISIEME TRAVAIL
- Suite 1 du cours: Nb Complexes
- Suite 2 du cours: Nb Complexes
- Suite 3 du cours: Nb Complexes
- Suite 4du cours:Nb Complexes
- Suite 5 du cours: Nb Complexes
- Suite 6 du cours:Nb COMPLEXES
- Suite 7 du cours: Nb COMPLEXES
- TEST 1 Nb COMPLEXES
- INFO TEST 1 Nb COMPLEXES
- TABLEAU D'HONNEUR TS2
- Devoir maison 1 du 24/09/10 TS
- AIDE1 DV n° 1 TS 24 sept 2010
- AIDE 2 DV n° 1 TS 24 sept 2010
- DS 1. 4/10/10 TS
- INFO DS n°1 6/10/10
- FEUILLE 1 D' EX. NOMBRE COMPLE
- INFO 1 FEUILLE 1 D'EX
- INFO 2 FEUILLE 1 EX NOMB. COMP
- INFO 3 FEUILLE 1 EX NOMB. COMP
- FEUILLE 2 D' EX. NB COMPLEXE
- LISTE 3 D'EX Nb COMPLEXES
- INFO 1 Liste 3 EX Nb COMPLEXES
- INFO 2 LISTE 3 EX Nb COMPLEXES
- INFO 3 LISTE 3 EX Nb COMPLEXES
TS DERIVATION DE COMP. DE FONCTIONS
- ALGORITHME DONNANT AVEC EULER
- DS n° 4 TS2 17 décembre 20
- INFO DS n° 4 TS2 17/12/11
- INFO EXERCICE TS2 16 /12/1
- INFO EX 77 DV maison TS2 05
- INFO EX 31 DV maison TS2 05
- INFO EX 36 DV MAISON TS2
- INFO EX 78 DV maison TS2 05
- ALGO EULER POUR LA COURBE D'UN
- EULER : PRGM TI 84
- DS n°5 TS2 EX 4 BAC BLC 12
- COURBE DE EXP AVEC ALGOBOX
- METHODE D'EULER POUR EXP AVEC
- INFO LISTE 1 D' EX DERIV. DE
- LISTE 2 D'EX DERIV. COMPOSEE
- INFO LISTE 2 D'EX DERIV. COM
- NOTES TS2 B BLC
- METHODE D'EULER POUR EXP
- LISTE 1 D' EX. DERIV. DE COMPO
TS...........Leçon n°8 CALCUL INTEGRAL 2
- Lien entre aire sous la courbe
- COURS PRIMITIVES
- Cours INTEGRATION Partie I
- Cours INTEGRATION: Partie II
- Algorithme d'encadrement d'une
- FEUILLE 1 D'EX. INTEGRATION
- INFO FEUILLE 1 D'EX : INTEGRAT
- FEUILLE n° 2 D'EXERCICES
- INFO FEUILLE n°2 D'EXERCICES:
- FEUILLE n° 3 D'EXERCICES
- INFO FEUILLE n ° 3 D' EXERCICE
- INFO LISTE 1 D'EX. PRIMITIVES
- INFO 1 DEVOIR MAISON: 11 mai 2
- DS n°9 15mai 2007 TS1
- INFO DS n°9 15 mai 2007 TS1
- LISTE 1 D ' EXERCICE : PRIMITI
- INFO DV n°9 TS1 15 mars 20
- EX 1 BAC BLANC TS 20 mars 201
- EX 2 BAC BLANC TS 20 mars 201
- EX 3 BAC BLANC TS 20 mars 201
- EX 4 BAC BLANC TS 20 mars 201
- Tableau d'honneur bac blanc du
- NOTES BAC BLANC TS 20 mars 201
- INFO DV n°10 TS1 11 avril
- INFO EX 7 DV n°10 TS1 du 11 a
- INFO EX1 DV n° 9 TS samedi
- INFO EX 2 DV n° 9 TS 7 mars
TS Leçon n° 9 GEOM. DANS L' ESPACE
- Cours: Positions relatives dan
- Othogonalité dans l'espace
- Rappels sur le produit scalair
- INFO1 EX DEVOIR MAISON juin
- EX figure avec géoplan
- INFO 2 DEVOIR MAISON: juin 201
- INFO 3 DEVOIR MAISON JUIN 2012
- EXERCICE DE BAC GEOM ESP
- INFO EX BAC GEOM ESP
- INFO DV n°10 18 mai 2013 TS
- Entraînement7 mai 2014 TS1
- INFO Entraînement 7mai 2014 T
- INFO EX1 DV n° 10 TS1 21 m
- INFO EX2 DV n° 10 TS1 21 mar
- INFO EX3 DV n° 10 TS1 21 mar
- DV n° 10 TS1 21 mars 2015
- INFO EX1 BAC BLANC 25 mars 201
- INFO EX 2 BAC BLANC 25 mars 20
- INFO EX3 BAC BLANC 25 mars 201
- INFO EX4 BAC BLANC 25 mars 201
- Image pour ex de bac
- DS TS1 du 18 / 4/ 15
- INFO EX 1 DS TS1 18 avril 2015
- INFO Ex 2 DS 18 avril 2015
- INFO EX 3 DS 18 avril 2015
- Travail à faire avril 2015 TS1
- INFO Travail à faire avril 201
- TABLEAU D'HONNEUR DS TS1 du 18
TS REVISIONS
- INFO EX 1 BAC JUIN 2012
- INFO EX 2 BAC JUIN 2012
- INFO EX 3 PARTIE A BAC J
- INFO EX 3 PARTIE B BAC J
- INFO EX 3 PARTIE C BAC J
- INFO DEBUT EX 4 BAC JUIN 20
- INFO FIN EX 4 BAC JUIN 2012
- EX BAC PROBA
- INFO EX PROBA BAC
- EXERCICE BAC CALCUL INTEGRAL
- INFO EX BAC CALCUL INTEGRAL
- ROC SUR LES SUITES
- EX 1 NOMBRES COMPLEXES
- EX2 NOMBRE COMPLEXES TS
- INFO EX2 BAC JUIN 2011
- INFO EXERCICE :Loi Binom. Loi
- EXERCICE: Loi Binom. et Expon
- INFO QCM :COMPLEXES TS
- QCM: COMPLEXES TS
- EXERCICE : Géométrie dans l'es
- ROC SUR LES SUITES
- EXERCICE SUR LES SUITES
- INFO EXERCICE SUR LES SUITES
- EXERCICE: Lois exponentielles
- INFO EXERCICE sur Les lois exp
SUJET DE BAC S juin 2019
- SUJET BAC mars 2023 Métropole
- SUJET BAC S Juin 2019
- EX1 Oblig. Juin 2019 INFO
- EX2 Oblig. Juin 2019 INFO
- EX3 Oblig. Juin 2019 INFO
- EX4 Oblig. Juin 2019 INFO
- EX4 spé math Juin 2019 INFO
- Commentaires sur bac S 2019
- Sujet EXERCICE 1 BAC 2018
- Sujet EXERCICE 2 BAC 2018
- Sujet EXERCICE 3 BAC 2018
- Sujet EXERCICE 4 Oblig. 2018
- Sujet EXERCICE 4 SPE 2018
- Corrigé bac S 2018 EXERCICE 1
- Corrigé bac S 2018 EXERCICE 2
- Corrigé bac S 2018 EXERCICE 3
- Corrigé EXERCICE 4 SPE 2018
- Corrigé bac S 2018 EXERCICE 4
- Commentaires sur le bac 2018
- EX 1 bac S 21 juin 2017
- EX 2 bac S 21 juin 2017
- EX 3 bac S 21 juin 2017
- EX 4 oblig bac S 21 juin 2017
- EX 4 bac S SPE 2017
- INFO EX 1 bac S 21 juin 2017
- INFO EX 2 bac S 21 juin 2017
- INFO EX 3 bac S 21 juin 2017
- INFO oblig EX 4 S 2017
- INFO EX 4 SPE Métropole 2017
- INFO EX 1 S 2016
- INFO EX 2 S 2016
- INFO EX 3 S Spé 2016
- INFO EX 4 S 2016
- TEST 26 janvier 2016
- Conseils.
- ESPRIT DE L'ORAL BAC S
- Exemple 1 de sujet d'oral S
- Exemple 2 de sujet d'oral S
- Exemple 3 de sujet d'oral S
- Exemple 4 de sujet d'oral S
- Exemple 5 de sujet d'oral S
- Exemple 6 de sujet d'oral S
- EXERCICE 1 sujet 2015
- EXERCICE 2 sujet 2015
- EXERCICE 3 sujet 2015
- EXERCICE 4 sujet 2015
- TABLEAU D'HONNEUR TS1 juin
- EXERCICE 1 BAC S 2014 S
- EXERCICE 2 BAC S 2014 S
- EXERCICE 3 BAC S 2014 S
- EXERCICE 4 BAC S 2014 S
- http://www.mathemaths.com/page
- Bac 2023
TS1 AP TS1
- AP 14/09/2013 TS1
- REVISIONS : bases algébriques
- INFO REVISIONS: bases alg.
- AP 21/09/2013 TS1
- AP 28/09/2013 TS1
- AP 05/10/2013 TS1
- FEUILLE D' EXERCICES REVISIO
- INFO FEUILLE D' EXERCICES REVI
- AP 12/10/2013 TS1
- AP 19/10/2013 TS1
- QUESTIONS SUR LES NOMBRES COM
- INFO QUESTIONS SUR LES NOMBRE
- AP 09/11/2013 TS1
- AP 16/11/2013 TS1
- AP 5 avril 2014 TS1
- AP du 2 oct. et 13 nov. 2014
- AP du 11 déc. 2014
- AP du jeudi 8 janvier 2015
- AP du jeudi 5 février 2015
- AP du jeudi 19 mars 2015
- AP du jeudi 16 avril 2015
- AP du jeudi 28 mai 2015
TS...........Leçon 1 SUITES
- 2.COURS Résumé : suite TS sept
- Leçon n°1 TS SEPT 2012
- Leçon n° 1 TS INFO ACTIVITE
- 3.COURS Résumé Suites TS sept
- 4.COURS Résumé SUITES TS
- Feuille 1d'ex suites
- 5. COURS SUITES TS SEPT 201
- INFO EX 1 Feuille d'ex sur les
- 6. COURS SUITES TS Sept 20
- INFO EX 2 Feuille d'ex sur les
- DV n°1 TS pour le 21/09/12
- INFO EX 3 Feuille d'ex sur les
- INFO EX 4 Feuille d'ex sur les
- INFO DV n° 1 SUITES TS Sept
- INFO EX 5 Feuille d'ex sur les
- AIDE pour le DV n°1 TS1 du 21/
- FEUILLE 2 d'ex suites TS
- EXERCICE 6
- INFO EX 1 Feuille 2 suites TS
- 1.COURS SUITES TS sept 2012
- INFO EX 2 Feuille 2 suites T
- INFO EX 3 Feuille 2 suites TS
- INFO EX 4 Feuille 2 suites T
- INFO EX 5 Feuille 2 suites TS
- LES R.O.C 1 sur les suites
- LES R.O.C 2 sur les suites
- LES R.O.C 3 sur les suites
- ROC 4 SUITES
- TEST 1 SUITES TS S
- INFO TEST n° 1 SUITES TS S
- BAC 2008 LIBAN Série S
- INFO 1 EX BAC 2008 LIBAN Série
- INFO 2 EX BAC 2008 LIBAN Série
- FEUILLE 3 d'ex suites TS
- INFO EX 1 FEUILLE 3 d'ex sur l
- INFO EX 2 FEUILLE 3 d'ex sur
- INFO EX 3 FEUILLE 3 d'exercice
- DV n° 2 TS pour le 05/10/12
- AIDE pour le DV n° 2 TS1 du 05
- EXERCICE : Suite géométrique
- EXERCICE : Suite récurrente TS
- EX 1:Sur les formes indétermin
- EX 2: Sur les formes indétermi
- EX 3: Sur les formes indétermi
- EXERCICES:WEB d'une suite TS S
- DS n°1 TS 29/09/12
- INFO EX 1 DS n° 1 TS 29 / 09 /
- INFO EX 2 DS 1 TS1 29 / 09/ 12
- AP2 du MATHS 29/ 09 /12
- INFO AP 2 du vendredi 28 sept
- EX en demi groupe 28/09/12
- INFO EX en demi groupe 28 / 09
- INFO EXERCICE 1 DV 2 TS 5/10/
- INFO EX 2 DV 2 TS1 5/10/12
- INFO EX 3 DV 2 TS 05/ 10/12
- Devoir n°1 TS1 16 septembre 20
- INFO DV n°1 TS1 16 sept 2014
- DV n° 2 TS1 27 sept 2014
- INFO DV n°2 TS1 27 sept 2014
- TEST de Cours : SUITES TS
- INFO TEST de Cours : SUITES
- Dv n° 3 TS1 maison 11 octobre
- INFO Dv n° 3 TS1 maison 11 oc
- INFO EX de bac 2014
- EX BAC 2014
- DS n° 1 TS1 4/10/14
- INFO DS n° 1 TS1 4/10/14
- Tableau d'honneur DS n° 1 TS1
TS SUITES
- Explications ludiques sur le raisonnement par récurrence
- INFO EXERCICE SUITE ET ARITHMETIQUE
- SUITE DE SOMMES PARTIELLES
- DS n° 6 TS2 13 fév 2012
- INFO EX 2 FIN DS n° 6 TS2 13/02/12
- TEST SUITES
- INFO TEST SUR LES SUITES
- TEST2 SUITES
- INFO TEST2 SUITE
- EXERCICE SUITE ET ARITHMETIQUE
- EXEMPLE D'ÉTUDE DES VARIATIONS D'UNE SUITE
- INFO ÉTUDE DU SENS DE VARIATION D'UNE SUITE
TS .......................Leçon n°6 TS Fonction ln et primitives
- Résumé sur la fonction ln
- COURS: Fonction ln
- COURS: PRIMITIVES
- FEUILLE n° 1 D'EXERCICES Ja
- FEUILLE n°2 D'EXERCICES janv
- INFO TEST EX Ln Exp TS1 26
- TEST sur ln et Exp TS1 Sam
- FEUILLE D'EX n°2 Primitives
- DS n° 6 TS1 9 février 2013
- INFO EX 1 DS n° 6 TS1 9 févrie
- INFO EX 2 Partie A DS n° 6 T
- INFO EXE 2 Partie B DS n° 6 T
- INFO EX 2 Partie C DS n° 6 sa
- INFO DEBUT EX 2 DV n°8 du 5
- INFO DV n°9 TS1 MARS 2013
- DS n° 5 TS1 samedi 10 janvier
- INFO Ds n°5 TS1 10 janvier 201
- TABLEAU D'HONNEUR DS n° 5 TS1
- INFO DV n° 7 TS 17 janvier 2
- DV n°7 TS 17 janvier 2015
Leçon.................n°7 Probabilité conditionnelle
- Cours : Proba.conditionnelles
- INFO LISTE D'EXERCICES 1
- LISTE D'EXERCICES 1
- INFO DV n° 8 TS 31 janvier 20
- DV n°8 TS 31 janvier 2015
- INFO EX1 BAC BLANC 12 février
- INFO EX 2 BAC BLANC 12 fév 201
- INFO EX3 BAC BLANC 12 fev 2015
- INFO EX 4 BAC BLANC fév 2015
- SUJET BAC BLANC 12 fév 2015
- Bac Blanc fév 2015 Tableau d'h
TS...........Leçon 2 COMPLEXES
- FEUILLE 1 d'ex sur les nombres
- INFO FEUILLE 1 sur les nombres
- DV n° 3 TS1 pour le 19/10/12
- AIDE 1 DV n °3 TS 19/10/12
- AIDE 2 DV n °3 TS 19/10/12
- EX BAC INDE AVRIL 2006
- INFO EX BAC S 2006 INDE
- FEUILLE n° 2. EX Nombres Compl
- INFO FEUILLE n ° 2 COMPLEXE
- INFO DV n° 3 TS 19 / 10/12
- FORMULAIRE TRIGO
- DV n° 4 TS pour le mardi 13 no
- DS n° 2 TS Samedi 27 octobre
- INFO DS n° 2 TS 27 oct. 2012
- INFO DV n°4 TS1 13nov 2012
- Activités sur les complexes
- DS n°2 8 /11/13 TS1
- INFO DS n°2 8 / 11/ 2013
- DV n° 4 TS1 20 novembre 2013
- TABLEAU D'HONNEUR DS n° 2 TS1
- INFO DV n° 4 TS1 mercredi 20 n
- Dv n° 4 TS1 maison 8 nov 2014
- INFO DV n°4 TS1 08 nov. 2014
- INFO DS n° 2 TS1 18/10/14
- DS n° 2 TS1 18/10/14
- AIDE DV n° 4 du 8 nov 2014 TS1
- Tableau d'honneur DS n° 2 TS1
- U inclus dans C
- Feuille 2 de U inclus dans C
- Activité sur U inclus dans C
- INFO ACTIVITE
- ACTIVITE 1
- INFO ACTIVITE 1
- EXEMPLE D'ACTIVITE MATHS EXP
- INFO ACTIVITE SUITE COMPLEXE
- INFO 2 ACTIVITE SUITE COMPLEXE
- LOGIQUE POUR RACINE DEUXIEME
- RACINE 2 ième de 1 + i DANS C
- THÈME : Résolution de Z ² + 2
- ENSEMBLE DE MANDELBROT
TS............Leçon n° 3 LIMITES CONTINUITE
- Leçon n° 3 Limites et continui
- DV n° 5 TS1 27 nov 2012
- EX bac . Th de la bijection
- EX sur le Th de la bijection
- DICHOTOMIE : PRGM TI 84
- Th valeurs intermédiaires
- Rappel et complément : Limites
- EX 2 DICHOTOMIE
- LISTE 1 D'EX LIMITE-CONTINUITE
- INFO LISTE1 EX LIM-CONT
- INFOTP 1 TS1 nov 2012 LI
- TP 1 TS1 novembre 2012
- LISTE1 d'exercices TS1 LIMIT
- DS n°3 TS1 Samedi 24 novembr
- INFO DS n° 3 TS1 Samedi 24
- INFO EX1 DV n°5 TS1 mardi 27
- INFO EX4 DV n°5 TS1 mardi 27
- INFO EX 3 DV n° 5 TS 1 27
- INFO EX2 DV n°5 TS1 27 novemb
- BULLETIN TRIM 1 déc 2012
- INFO TEST : Limite, Continuité
- Test: Limite Continuité Th de
- DS n° 3 TS1 vendredi 22 nov.
- INFO DS n° 3 TS1 vendredi 22
- TABLEAU D'HONNEUR DS n° 3 TS
- TS1 Moyenne provisoire au 26 n
- DICHO Avec la Casio
- INFO 3 FEUILLE 1 SUR LES NOMBR
TS ...................Leçon.n°5 TS Fonction Exp
- Résumé sur la fonction exp
- FEUILLE D'EX sur les prop de l
- INFO FEUILLE D'EX sur les pro
- FEUILLE D'EX n°2 fonction ex
- INFO FEUILLE D'EX n°2 Fonction
- FEUILLE n° 1 EX FONCTION EXP
- INFO EX1 FEUILLE 1 FONCTION
- INFO EX2 FEUILLE 1 Fonction
- INFO EX3 FEUILLE 1 Fonction E
- INFO EX4 FEUILLE 1 FONCT
- INFO EX5 FEUILLE 1 FONCTION E
- INFO EX 6 FEUILLE 1 FONC
- TS1 DS n°4 TS1 22 décembre 2
- INFO EX1 DS n° 4 TS1 22 décemb
- INFO EX 2 DS n °4 TS1 2012
- INFO EX3 DS n° 4 TS1 22 décemb
- DV n° 7 TS1 12 janvier 201
- EX1 DV n° 7 TS1
- INFO EX 1 DV n°7 TS1 12 /
- EX 2 DV n° 7 TS1 12 /01/13
- INFO EX2 DV n° 7 TS1 12/01/13
- INFO EX3 DV n°7 TS1 12 /01/1
- EXERCICE 3 DV n°7 TS1 12/01
- INFO EX 4 DV n° 7 TS1 12 / 0
- EX 4 DV n° 7 TS1 12/01/13
- INFO EX 5 DV n° 7 TS1 12
- EXERCICE 5 DV n° 7 TS1 12
- INFO EX 6 DV n°7 TS1 12
- EX 6 DV n° 7 TS1 12 / 01
- DV n° 6 TS1 pour le 8 janvie
- FEUILLE D'EXERCICE n°2 Leçon
- INFO DS n° 4 21 /12/13 TS1
- DS n° 4 21/12/13 TS1
- TABLEAU D'HONNEUR DS n° 4 TS1
- INFO DV n° 6 TS1 8/01/14
- DV n° 7 TS1 pour le 22 janvi
- TEST 15 janvier2014 TS1
- INFO TEST 15 janv.2014 TS1
- TABLEAU D'HONNEUR DS n° 5 TS
- INFO EX 1 DV n°7 TS1 22 ja
- INFO EX 2 DV n° 7 22/1/14
- INFO EX3 DV n° 7 22/1/14 TS1
- AIDE DV n° 7 du 22 / 1/ 14
- Plan Salle 112
- INFO EX 1 Dv n° 6 TS1 13 déc
- INFO EX 2 DV n° 6 du 13 déc.
- INFO EX 3 et 4 DV n° 6 du 13
- PARTIE B d'un ex de bac S juin
- DS n° 4 TS1 13/12/14
- INFO DS n° 4 13/12/14 TS1
- TABLEAU D'HONNEUR DS n° 4 TS1
TS............Leçon n° 4 COMPLEMENT DERIVATION
- COURS: DERIVATION DE LA COMPOS
- DV n° 6 TS1 18 décembre 201
- INFO EX1 DV n°6 TS1 mardi 18
- INFO EX 3 DV n°6 TS1 mardi 1
- INFO EX 2 DV n°6 TS1 M
- INFO FEUILLE D'EXERCICE n°1 L
- FEUILLE D'EXERCICE n°1
- EXERCICES
- Moyenne TRIM 1 TS1 déc. 2013
- INFO DV n°5 TS1 6 déc. 201
- Feuille d'ex Leçons 3 et 4 TS
- INFO DS n° 3 15/11/14 TS1
- DS n° 3 15 / 11 / 14 TS1
- Dv n° 5 TS1 maison 22 nov 201
- Tableau d'honneur DS n° 3 TS1
- INFO Dv n° 5 TS1 maison 22 o
- BULLETIN TRIM 1 Nov 2014
- INFO FEUILLE D'EXERCICES
- FEUILLE D'EXERCICES TS1 13
- INFO EX SUR LA METHODE D'EU
- EX SUR LA METHODE D'EULER
- Exercice sur les sinus et cosi
TES Spécialité math.
- INFO 2 DV n° 2 Maison TES spé
- INFO EX BAC SPE 29 MARS 2012
- EX BAC BLANC TES SPE 29 MARS2012
- DV Maison TES EX 2 Partie 3 Lundi 6 février 2012
- DV Maison TES EX 2 PARTIE 1 Lundi 6 février 2012
- DV Maison TES INFO SECONDE PARTIE DE EX 2 Lundi 6 février 2012
- TEST TES DU 30 JANVIER 2012
- INFO EX BAC ES ANTILLES-GUYANE
- EX BAC ES ANTILLES-GUYANE2007 SUITES
- EXERCICE SPE MATH
- INFO EXERCICE BAC ES spé
- INFO DS n° 4 TES 12/12/11
- DS n° 4 TES 12 décembre 2011
- INFO 1 DV n° 2 Maison TES Spé
- TD 1sur les surfaces TES Spé
- DS n° 3 Spé TES 14/11/11
- TEST GEOMETRIE DANS L'ESPACE
- INFO TEST 1 SPE MATH TES
- EXERCICE matrices et graphe TES spé
- INFO EX 4 BAC ES SPE 2013
TES 2012 ; 2013 ; 2014 spécialité
- ACTIVITE MATRICES TES SPE MATH
- Problème TES OCT 2013
- EX : Leçon Matrices
- DSn°1 TES SPE 08 / 10 /12
- INFO Problème TES OCT 2013
- DS n°1 TES spé 14 / 10/2013
- INFO DS n° 1 TES SPE 14 oct 2
- TABLEAU D'HONNEUR DS n° 1 TES
- MODELISER EX 1
- INFO TEST n° 2 TES SPE 18 nov
- TEST n° 2 TES SPE du 18 novem
- Notes
- MOORE TES Déc.2013
- INFO DS n° 1 8 /10/12 TES s
- INFO Problème1 bac ES spé
- Problèmes bac ES spé
- INFO Problèmes 2 bac ES spé
- INFOTEST TES Spé décembre 2011
- TEST TES spé décembre 2011
- INFO DS n° 2 TES SPE 18 no
- TES DS n°2 spé maths 18 nov
- TEST TES Spé 10 décembre 2012
- INFO EX 1 TEST TES 10 décembr
- INFO EX2 TEST TES Spé 10 Déc 2
- NOTES DU DS n° 3 du 16 / 12 /
- Moore-DijKstra Pondichéry
- TABLEAU Moore-Dijkstra Asie
- TABLEAU Moore-Dijkstra Polynés
- EXERCICE SURE LES GRAPHES
- EXERCICE 4 SUR LES GRAPHES
- INFO DS n°4 TES spé maths 27
- NOTES DU DS n° 4 du 27 / 011 /
- TES DS n°4 spé maths 27 janv
- INFO EXERCICE de bac du TEST
- NOTES TRIM 2 TES SPE
- Bac Blanc EX SPE TES 21 mars
- Notes EX spé. math. Bac blanc
- EX DE BAC Tableau de Moore
- France Métropolitaine TES 2
- EX Bac ES Pondichéry 2013
- Travail à faire pour s'entraîn
- Test des bases de cours:
- Test des bases de cours
- INFO EX BAC LIBAN 2014 ES spé
- EX BAC LIBAN 2014 spé maths
- INFO Feuille d'ex TES sur les
- DS n° 1 TES spé 13/10/14
- INFO DS n ° 1 TES spé 13 /10 2
- DV maison 10 nov 2014 TES Spé
- INFO TEST TES SPE 01/12/14
- TEST TES SPE 01/12/14
- INFO EX spé bac 2009
- EX DE BAC ES SPE 2009
- INFO TEST 9 décembre 2013
- TEST du 9 déc 2013
- EX BAC SPE 2014 ES Métropole
- SUJET SPE 2014
- INFO TEST SPE MATH. 26 janvi
- TEST TES SPE 26/1/15
- INFO BAC BLANC 13 février 201
- Tableau d'honneur bac blanc T
- Ex bac ES Pondichéry avril 2
- Texte complet de l'exercice du
- EX1 bac ES 2015
- EX2 bac ES 2015
- EX4 bac ES 2015
TS....... Leçon sur les PROBABILITES
- INFO TEST EX de bac donné le
- NOTES DU TEST TS 08/02/14
- V.a.r indépendantes
- TS1 INFO EX1 BAC BLANC 15 fév2
- TS1 INFO EX2 2 BAC BLANC 15 fé
- TS INFO EX 3 BAC BLANC TS 15/2
- TS INFO EX4 BAC BLANC TS 15/2/
- FIN DE L'EXERCICE DE RÉVISION
- Tableau d'honneur bac blanc du
- INFO DV n°8 TS1 5 mars 201
- AIDE 1 DV n ° 8 à la maison TS
- AIDE 2 DV n ° 8 à la maison
- AIDE 3 DV n ° 8 à la maison T
- MOYENNE TRIM 2 TS1
INFO 1 DV n° 7 1S 27 mars 2010
INFO 1 DV n ° 7 1S1 du 27 mars 2010 reporté au 17 /04 /10
EXERCICE 1
Le plan est muni d'un repère orthonormal ( O ; vect ( i ) , vect( j ) ) .
( Unité graphique : 1 cm )
Soit la fonction f : x → ( x² - 3 x ) / ( x + 1 ) définie dans IR- { - 1 }.
Soit C sa courbe représentative.
1. Trouver sa fonction dérivée f '.
On a : f = u / v
avec u : x → x² - 3 x et v : x → x + 1 .
u et v sont deux fonctions définies et dérivables
sur IR - { - 1 } avec v non nulle sur IR - { - 1 }.
Donc f est définie et dérivable dans IR - { - 1 }.
On a : f ' = ( u / v )' = ( v u ' - u v ' ) / v²
On a : u ' : x → 2 x - 3 et v : x → 1
Soit x dans IR - { - 1 } .
On a :
f ' ( x ) = [( x + 1 ) ( 2 x - 3 ) - ( x² - 3 x ) 1 ] /( x + 1 )2
c'est-à-dire
f ' ( x ) = [ 2 x² - 3 x + 2 x - 3 - x² + 3 x ] /( x + 1 )2
c'est-à-dire
f ' ( x ) = ( x² + 2x - 3 ) / ( x + 1 )2
2. Donner le signe de f '( x ) suivant x dans IR- { - 1 }.
f '( x ) est un quotient dont le dénominateur est strictement positif
pour tout x dans IR - { - 1 }.
f '( x ) est donc le signe du numérateur .
x² + 2x - 3 admet 1 comme racine évidente.
L'autre racine est donc c / a = - 3.
La règle des signes d'un trinome du second degré
permet de donner le signe de x² + 2x - 3 .
a = 1
Donc a > 0
Conclusion:
| x | - ∞ -3 -1 1 + ∞ |
| f ' ( x ) | + 0 - || - 0 + |
3. Dresser le tableau de variation de f.
| x | - ∞ -3 -1 1 + ∞ |
| f '(x) | + 0 - || - 0 + |
| f( x ) | ↑ -9 ↓ || ↓ - 1 ↑ |
4. a. Déterminer f( x ) - ( x - 4 ) pour tout x dans IR.
On peut utiliser d'abord la division:
x² - 3 x
| x + 1
- ( x2 + x )
| x - 4
- 4 x
|
- ( - 4 x - 4 )
|
4
Ainsi :
x² - 3 x = ( x - 4 ) ( x + 1 ) + 4
Donc:
( x² - 3 x / ( x + 1) = x - 4 + 4 / ( x + 1 ) pour tout x dans IR - { - 1}.
Conclusion:
f( x ) = x - 4 + 4 / ( x + 1 ) pour tout x dans IR - { - 1}.
b. Montrer que lim ( f( x ) - ( x - 4 ) ) = 0
x → + ∞
Que peut-on en déduire pour la courbe ( C ) de f en + ∞ ?
On a vu que :
f ( x ) = x - 4 + 4 / ( x + 1 ) pour tout x dans IR - { - 1}.
Donc : f( x ) - ( x - 4 ) = 4 / ( x + 1 ) pour tout x dans IR - { - 1}
Or : lim 4 / ( x + 1 ) = 0
x → + ∞
D'où :
lim ( f( x ) - ( x - 4 ) ) = 0
Conclusion: La courbe de f admet une asymptote oblique d'équation y = x - 4 en + ∞.
c.Tracer la courbe ( C ) de f ainsi que les droites D: y = x - 4 et
D ' : x = - 1 dans le même repère.
Les deux droites D et D ' sont deux asymptotes pour la courbe de f.
Il est impératif de les tracer même quand ce n'est pas demandé.
En effet la courbe s'en rapproche. C'est donc une précieuse indication.
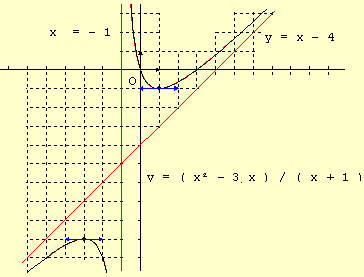
5. Donner une équation de la tangente T à ( C ) au point d'abscisse 2.
Considérons y = f ' (a ) ( x - a ) + f( a ) avec a = 2.
On a :
f ' ( 2 ) = ( 2² + 2 × 2 - 3 ) / ( 2 + 1 )²
c-à-d f '( 2 ) = 5 / 9
f( 2 ) = - 2 / 3
En reportant on a :
y = ( 5 / 9 ) ( x - 2 ) - 2 / 3
c-à-d y = ( 5 / 9 ) x - 10 / 9 - 6 / 9
c-à-d y = ( 5 / 9 ) x - 16 / 9
Conclusion: La tangente T à la courbe de f a comme équation réduite
y = ( 5 / 9 ) x - 16 / 9
6. Soit K le point d'intersection des droites D et D '.
Considérons le système des deux équations des deux droites D et D '
pour obtenir les coordonnées de K.
y = x - 4
x = - 1 On obtient : x = - 1 y = - 5 Conclusion: Le point recherché est K ( - 1 ; - 5 ) . a. Donner la nouvelle équation de ( C ) dans le nouveau repère Dans le repère d'origne O l'équation de ( C ) est y = f( x ). Dans le nouveau repère d'origine K l'équation de ( C ) sera Y = g( X ). Remplaçons x et y dans y = f( x ) c-à-d dans y = x - 4 + 4 / ( x + 1 ) avec x distinct de - 1 à l'aide des formules de changement de repère par changement d'origine: x = xK + X c-à-d x = - 1 + X y = yK + Y c-à-d y =- 5 + Y On obtient : - 5 + Y = - 1 + X - 4 + 4 / ( - 1+ X + 1 ) avec X non nul Y = X + 4 / X avec X non nul On pose : g( X ) = X + 4 / X Conclusion: La nouvelle équation Y = X + 4 / X est avec X non nul b. Etudier la parité de la fonction g. g est-elle impaire . En effet: Son domaine de définition IR* est centré en 0 . De plus : g( - X ) = - g ( X ) pour tout x dans IR* . car g( - X ) = - X + 4 / ( - X ) = - ( X + 4 / X ) = - g( X ) En déduire une particularité de la courbe ( C ) de g. On peut alors dire que point K est une centre de symétrie de la courbe de g donc de la courbe de f. 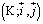 .
.